
- Автор Miles Stephen stephen@answers-science.com.
- Public 2024-01-18 08:18.
- Последнее изменение 2025-01-22 17:08.
Скалярное произведение удовлетворяет следующим свойствам, если a, b и c - действительные векторы, а r - скаляр
- Коммутативный: который следует из определения (θ - угол между a и b):
- Дистрибутивное сложение над вектором:
- Билинейный:
- Скалярный умножение:
Впоследствии можно также спросить, каковы 4 свойства скалярного произведения?
Свойства точечного продукта
- u · v = | u || v | cos θ
- u · v = v · u.
- u · v = 0, когда u и v ортогональны.
- 0 · 0 = 0.
- | v |2 = v · v.
- а (и · v) = (а и) · v.
- (au + bv) · w = (au) · w + (bv) · w.
Можно также спросить, каковы свойства кросс-произведения? Свойства перекрестного продукта:
- Длина произведения двух векторов равна.
- Длина векторного произведения двух векторов равна площади параллелограмма, определяемой двумя векторами (см. Рисунок ниже).
- Антикоммутативность:
- Умножение на скаляры:
- Распределительность:
Точно так же вы можете спросить, что означает скалярный продукт?
А скалярное произведение это скаляр ценить это это результат работы двух векторов с одинаковым количеством компонентов. Для двух векторов A и B, каждый из которых имеет n компонентов, скалярное произведение рассчитывается как: A · B = A1B1 + + А B . В скалярное произведение таким образом, сумма продукты каждого компонента двух векторов.
Каковы свойства векторов?
Алгебраические свойства векторов
- Коммутативный (вектор) P + Q = Q + P.
- Ассоциативный (вектор) (P + Q) + R = P + (Q + R)
- Аддитивное тождество Есть вектор 0 такой.
- Аддитивно обратный Для любого P существует вектор -P такой, что P + (-P) = 0.
- Распределительный (вектор) r (P + Q) = rP + rQ.
- Распределительный (скалярный) (r + s) P = rP + sP.
- Ассоциативный (скалярный) r (sP) = (rs) P.
Рекомендуемые:
Каковы физические свойства элементов группы 2?

Элементы, включенные в эту группу, включают бериллий, магний, кальций, стронций, барий и радий. Физические свойства: Физическая природа: атомный объем и радиус: Плотность: Точки плавления и кипения: Энергия ионизации: Состояние окисления: Электроположительность: Электроотрицательность:
Каковы физические свойства викторины материи?

Характеристика чистого вещества, которую можно наблюдать, не превращая ее в другое вещество, например: цвет, текстура, плотность, форма кристалла, точка кипения и точка замерзания и т. Д. Измерение количества вещества, содержащегося в объекте, в граммах. Количество места, которое что-то занимает
Каковы свойства температуры?

Температура - это величина, измеряемая термометром. Температура связана со средней кинетической энергией атомов и молекул в системе. Абсолютный ноль - это температура, при которой движение молекул отсутствует. Существует три основных температурных шкалы: Цельсия, Фаренгейта и Кельвина
Каковы физические свойства цезия?

Физические свойства Цезий - серебристо-белый блестящий металл, очень мягкий и пластичный. Под пластичностью подразумевается, что его можно втягивать в тонкую проволоку. Его температура плавления составляет 28,5 ° C (83,3 ° F). Он легко тает в тепле рук, но никогда не следует обращаться с ним подобным образом
Как вы рассчитываете корреляцию момента произведения Пирсона в SPSS?
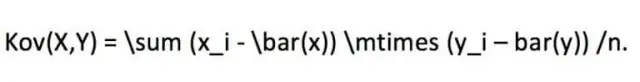
Чтобы запустить двумерную корреляцию Пирсона, щелкните Анализировать> Корреляция> Двумерная корреляция. Выберите переменные Высота и Вес и переместите их в поле Переменные. В области «Коэффициенты корреляции» выберите «Пирсон». В области «Проверка значимости» выберите желаемый критерий значимости, двусторонний или односторонний
