Оглавление:
Видео: Как вы находите точки пересечения неравенства?
2024 Автор: Miles Stephen | [email protected]. Последнее изменение: 2023-12-15 23:40
В качестве альтернативы мы можем определить x- перехватить И они- перехватить стандартной формы линейный неравенство подставив y = 0, затем решите относительно x и подставив x = 0, затем решите относительно y соответственно. Напомним, что х- перехватить это значение x, когда y = 0, и они- перехватить - значение y при x = 0.
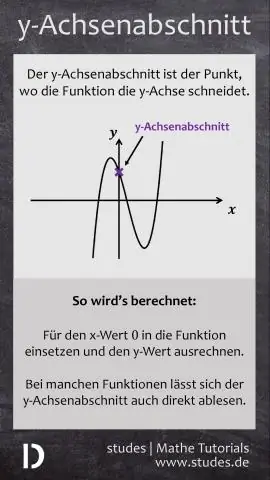
Отсюда, как найти точку пересечения неравенства по оси Y?
Вы можете найти в у - перехватить посмотрев на график и увидев, какая точка пересекает у ось. У этой точки всегда будет Икс координата нуля. способ найти в у - перехватить , если ты знать уравнение у - перехватить является решением уравнения, когда Икс = 0. Давайте найти уравнение для этой линии.
Кроме того, как изменить линейные неравенства? Как построить график линейного неравенства
- Переставьте уравнение так, чтобы «y» было слева, а все остальное - справа.
- Постройте линию "y =" (сделайте ее сплошной линией для y≤ ory≥ и пунктирной линией для y)
- Заштрихуйте над линией для «больше чем» (y> или y≥) или ниже линии для «меньше чем» (y <или y≤).
Таким образом, каковы решения неравенства?
"Решение" неравенство означает найти все его решения . А " решение '' из неравенство число, которое при замене переменной делает неравенство верное заявление. Когда мы подставляем 8 вместо x, неравенство становится 8-2> 5. Таким образом, x = 8 является решение в неравенство.
Как решить квадратные неравенства?
Чтобы решить квадратное неравенство, выполните следующие действия:
- Решите неравенство, как если бы это было уравнение.
- Обведите граничные точки сплошными кружками, если исходное неравенство включает равенство; в противном случае сделайте граничные точки открытыми кругами.
- Выберите точки из каждой области, созданной граничными точками.
Рекомендуемые:
Может ли быть более одной точки пересечения графиков двух линейных уравнений?
Если графики двух линейных уравнений не совпадают, может быть только одна точка пересечения, потому что две прямые могут пересекаться не более чем в одной точке. Из этой точки переместите на одну единицу вправо и вертикально переместите значение уклона, чтобы построить вторую точку. Затем соедините две точки
Как вы изобразите неравенства на координатной плоскости?
Есть три шага: переставьте уравнение так, чтобы «y» находилось слева, а все остальное - справа. Постройте линию 'y =' (сделайте ее сплошной линией для y≤ или y≥ и пунктирной линией для y). Заштрихуйте линию над линией для «больше чем» (y> или y≥) или ниже линии для 'меньше чем' (y <или y≤)
Как написать стандартную форму пересечения уклона?
Стандартная форма - это еще один способ записать форму пересечения наклона (в отличие от y = mx + b). Он записывается как Ax + By = C. Вы также можете изменить форму пересечения наклона на стандартную форму следующим образом: Y = -3 / 2x + 3. Затем вы изолируете точку пересечения оси y (в данном случае это 2) следующим образом: добавьте 3 / 2x к каждой стороне уравнения, чтобы получить: 3 / 2x + y = 3
Как найти точку пересечения наклона по таблице?
Чтобы найти точку пересечения по оси Y, подставьте наклон вместо m в формуле y = mx + b и подставьте заданную упорядоченную пару в таблице для x и y в формуле, затем решите для b. Наконец, подставьте значения для m и b в формулу y = mx + b, чтобы записать уравнение линии
Как написать уравнение таблицы в форме пересечения наклона?
Возьмите уравнение y = mx + b и вставьте значение m (m = 1) и пару координат (x, y) из таблицы, например (5, 3). Затем решите относительно b. Наконец, используйте найденные вами значения m и b (m = 1 и b = -2), чтобы написать уравнение