
Оглавление:
- Автор Miles Stephen [email protected].
- Public 2024-01-18 08:18.
- Последнее изменение 2025-01-22 17:08.
Примеры бесконечного множества:
- Установленный всех точек на плоскости есть бесконечный набор .
- Установленный всех точек в линейном сегменте - это бесконечный набор .
- Установленный всех положительных целых чисел, кратных 3, является бесконечный набор .
- W = {0, 1, 2, 3, ……..} т.е. установленный всех целых чисел бесконечный набор .
- N = {1, 2, 3, ……….}
- Z = {………
Точно так же вы можете спросить, как вы показываете бесконечное множество?
Вы можете доказать, что множество бесконечно, просто продемонстрировав две вещи:
- Для данного n он имеет хотя бы один элемент длины n.
- Если он имеет элемент максимальной конечной длины, то вы можете построить более длинный элемент (тем самым опровергая, что элемент максимальной конечной длины).
Во-вторых, как определить, является ли набор бесконечным или конечным? Пункты для определения множества как конечного или бесконечного:
- Если у набора есть как начальная, так и конечная точки, тогда он конечен, но если у него нет начальной или конечной точки, то это бесконечное множество.
- Если набор имеет ограниченное количество элементов, то он конечен, но если его количество элементов неограниченно, то оно бесконечно.
Во-вторых, что такое конечное и бесконечное множество с примером?
Примеры из Бесконечные наборы Если установленный это не конечный набор , то это бесконечный набор . Натуральные числа и целые числа - два Примеры из наборы которые бесконечный и, следовательно, не конечный . Жирная заглавная буква Z часто используется для обозначения установленный целых чисел.
Существуют ли бесконечные множества?
Нет бесконечные множества . Не только делать бесконечные наборы нет существовать , но само понятие логически противоречиво - ничем не отличается от «квадратных кругов». Бесконечные множества буквально закреплены в современных основах математики - с так называемой «Аксиомой математики». бесконечность ”.
Рекомендуемые:
Как написать формулу соединения, содержащего многоатомный ион?
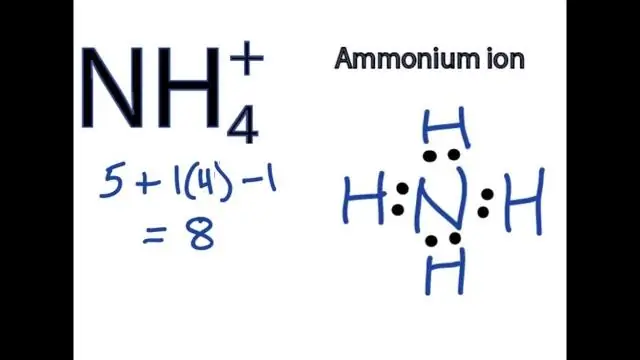
Чтобы написать формулы для соединений, содержащих многоатомные ионы, напишите символ для иона металла, а затем формулу для многоатомного иона и сбалансируйте заряды. Чтобы назвать соединение, содержащее многоатомный ион, сначала укажите катион, а затем анион
Как написать уравнение в форме углового коэффициента с учетом двух точек?

Существуют различные формы, в которых мы можем записать уравнение прямой: форма точки-уклона, форма уклона-пересечения, стандартная форма и т. Д. Уравнение прямой, заданное двумя точками (x1, y1) и (x2, y2). ), через который проходит линия, задается формулой ((y - y1) / (x - x1)) / ((y2 - y1) / (x2 - x1))
Как написать суровость?

Прилагательное, серьезный, серьезный. жесткий; излишне экстремальный: суровая критика; суровые законы. серьезный или суровый в манерах или внешнем виде: суровое лицо. могила; критическое: тяжелое заболевание. трудно вынести, выполнить, выполнить и т.д .: суровое испытание своих сил
Какое картографирование объединяет множество традиционных типов карт в одну?

Что такое ГИС? Сочетает в себе многие из описанных традиционных типов стилей отображения
Как написать что-то как функцию?

Вы пишете функции с именем функции, за которым следует зависимая переменная, например, f (x), g (x) или даже h (t), если функция зависит от времени. Вы читаете функцию f (x) как «f из x», а h (t) как «h из t». Функции не обязательно должны быть линейными
