Видео: В чем разница между средним значением и дисперсией?
2024 Автор: Miles Stephen | [email protected]. Последнее изменение: 2023-12-15 23:40
Что разница между средним и дисперсией ? Проще говоря: иметь в виду это арифметика в среднем всех чисел, арифметика иметь в виду . В отклонение - это число, которое дает нам представление о том, насколько странными могут быть эти числа, другими словами, мера того, насколько они различаются.
Имея это в виду, как вы находите дисперсию различий?
Дисперсия определяется как среднее квадратов отклонений от среднего. Для расчета отклонение , вы сначала вычитаете среднее значение из каждого числа, а затем возводите результат в квадрат найти квадрат различия . Ты тогда найти среднее значение квадратов различия . Результат - это отклонение.
Кроме того, что означает выборочная дисперсия? Определение из Выборочная дисперсия В отклонение математически определяется как среднее значение квадратов отличий от иметь в виду . Шаг 2: вычтите иметь в виду и возведите результат в квадрат.
Точно так же спрашивают, о чем нам говорит дисперсия?
Дисперсия измеряет, насколько распространен набор данных. А отклонение нуля означает, что все значения идентичны. Все ненулевые отклонения положительные. Дисперсия является средним квадратом расстояний от каждой точки до среднего.
Почему важна дисперсия?
Это чрезвычайно важный как средство визуализации и понимания рассматриваемых данных. Статистические данные в некотором смысле созданы для представления данных в виде двух или трех чисел. В отклонение является мерой того, насколько рассредоточены или распространены множества, для чего «среднее» (среднее или медианное значение) не предназначено.
Рекомендуемые:
В чем разница между диффузией осмоса и облегченной диффузией?
Осмос также возникает, когда вода перемещается из одной ячейки в другую. С другой стороны, облегченная диффузия происходит, когда среда, окружающая клетку, имеет более высокую концентрацию ионов или молекул, чем среда внутри клетки. Молекулы перемещаются из окружающей среды в клетку за счет градиента диффузии
В чем разница между корреляцией и хи-квадрат?
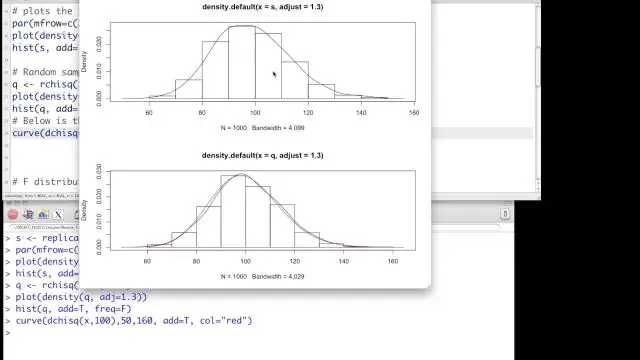
Итак, корреляция - это линейная связь между двумя переменными. Обычно оба являются непрерывными (или почти непрерывными), но есть вариации для случая, когда один является дихотомическим. Хи-квадрат обычно говорит о независимости двух переменных. Обычно оба категоричны
В чем разница между климатической зоной и биомом?
Климат классифицируется на основе температуры атмосферы и количества осадков, тогда как биом классифицируется в первую очередь на основе однородных типов растительности. Климат может определять, какой биом присутствует, но биом обычно не контролирует или влияет на климат таким же образом
Как органические соединения получили свое название? Как это слово связано со своим значением?
Как это слово связано со своим значением? Органические соединения получили свое название от количества углеродных связей. Слово связано со значением, потому что оно связано со связями в атомах углерода в органических соединениях
В чем разница между дипольным диполем и лондонской дисперсией?
Хотя все молекулы притягиваются друг к другу, одни притяжения сильнее других. Неполярные молекулы притягиваются дисперсионным притяжением Лондона; полярные молекулы притягиваются как за счет лондонской дисперсионной силы, так и за счет более сильного диполь-дипольного притяжения