Видео: Как вы определяете конечное поведение многочлена?
2024 Автор: Miles Stephen | [email protected]. Последнее изменение: 2023-12-15 23:40
Тогда коэффициент ведущего члена будет определять в поведение принадлежащий многочлен . Если переменная (скажем, X) отрицательна, то X в члене наивысшей степени создает отрицательное значение. Затем мы умножаем коэффициент ведущего члена на отрицательный, чтобы определить конечное поведение.
Также нужно знать, как вы определяете поведение левого и правого концов?
Используйте тест опережающего коэффициента, чтобы определять в конец поведения графика полиномиальной функции f (x) = - x3 + 5x. Решение: поскольку степень нечетная, а старший коэффициент отрицательный, график поднимается до левый и падает на Правильно как показано на рисунке.
Кроме того, как вы находите асимптоты? Вертикаль асимптоты произойдет при тех значениях x, для которых знаменатель равен нулю: x - 1 = 0 x = 1 Таким образом, график будет иметь вертикальную асимптота при x = 1. Чтобы найти горизонтальный асимптота , отметим, что степень числителя равна двум, а степень знаменателя равна единице.
Соответственно, как вы определяете конечное поведение?
В конец поведения функции f описывает поведение графика функции на «концах» оси абсцисс. Другими словами, конец поведения функции описывает тенденцию графика, если мы посмотрим вправо конец оси x (когда x приближается к + ∞) и влево конец оси x (когда x приближается к −∞).
Что такое конечное поведение?
В конец поведения графа определяется как то, что происходит на концах каждого графа. Когда функция приближается к положительной или отрицательной бесконечности, главный член определяет, как будет выглядеть график при движении к бесконечности.
Рекомендуемые:
Как вы определяете логическую переменную?
Логические переменные - это переменные, которые могут иметь только два возможных значения: истина и ложь. Чтобы объявить логическую переменную, мы используем ключевое слово bool. bool b; Чтобы инициализировать или присвоить логической переменной значение true или false, мы используем ключевые слова true и false
Как вы определяете элементы и соединения?
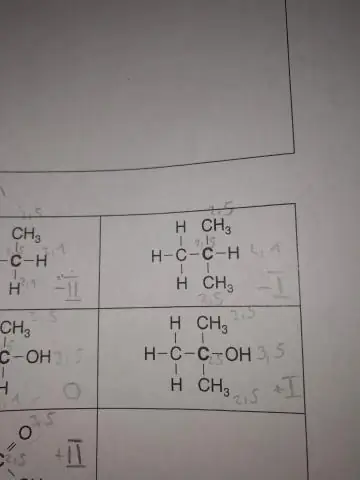
Проще говоря, элементы состоят только из одного вида атомов, которые нельзя разделить. Соединения состоят из атомов двух или более элементов, связанных вместе, и могут быть разбиты на простой тип вещества химическим путем
Как вы определяете приоритет хиральности?
1. Установите приоритет четырех атомов или групп атомов, присоединенных к хиральному центру, на основе атомного номера атома, который связан непосредственно с хиральным центром. Чем выше атомный номер, тем выше приоритет. «4» имеет самый низкий приоритет
Каково конечное поведение полиномиальной функции Brainly?
График с левым концом вниз и правым концом вверх. ведущий коэффициент отрицательный, тогда левый конец вверх, а правый конец вниз. Следовательно, полиномиальная функция имеет нечетную степень, а старший коэффициент отрицателен
Как вы находите ведущий коэффициент и конечное поведение?
Если переменная (скажем, X) отрицательна, то X в члене наивысшей степени создает отрицательное значение. Затем мы умножаем коэффициент ведущего члена на отрицательный, чтобы определить конечное поведение