Оглавление:
Видео: Как рассчитать нелинейную регрессию?
2024 Автор: Miles Stephen | [email protected]. Последнее изменение: 2023-12-15 23:40
Если твой модель использует уравнение в виде Y = a0 + b1Икс1, это модель линейной регрессии . Если нет, то это нелинейный.
Y = f (X, β) + ε
- X = вектор из p предикторов,
- β = вектор k параметров,
- f (-) = известное регресс функция
- ε = член ошибки.
Точно так же спрашивается, что такое модель нелинейной регрессии?
В статистике нелинейная регрессия это форма регрессионный анализ в котором данные наблюдений моделируются функцией что является нелинейным сочетание модель параметры и зависит от одной или нескольких независимых переменных. Данные аппроксимированы методом последовательных приближений.
Во-вторых, для чего используется нелинейная регрессия? Нелинейная регрессия это форма регресс анализ, при котором данные соответствуют модели и затем выражаются в виде математической функции. Использование нелинейной регрессии логарифмические функции, тригонометрические функции, экспоненциальные функции и другие методы подбора.
Таким образом, как определить линейную или нелинейную регрессию?
А линейная регрессия уравнение просто суммирует члены. В то время как модель должно быть линейный в параметрах вы можете поднять независимую переменную на показатель степени, чтобы она соответствовала кривой. Например, вы можете включить член в квадрате или кубе. Нелинейная регрессия модели - это все, что не следует этой единственной форме.
Какие бывают типы регрессии?
Типы регрессии
- Линейная регрессия. Это простейшая форма регрессии.
- Полиномиальная регрессия. Это метод подбора нелинейного уравнения путем взятия полиномиальных функций от независимой переменной.
- Логистическая регрессия.
- Квантильная регрессия.
- Хребтовая регрессия.
- Лассо-регрессия.
- Эластичная чистая регрессия.
- Регрессия основных компонентов (ПЦР)
Рекомендуемые:
Как сделать синусоидальную регрессию на калькуляторе?
ВИДЕО Итак, как вы рассчитываете синусоидальную регрессию? Синусоидальная регрессия . Отрегулируйте значения A, B, C и D в уравнение y = A * sin (B (x-C)) + D, чтобы получить синусоидальный Кривая соответствует заданному набору случайно сгенерированных данных.
Что вызывает морскую регрессию?
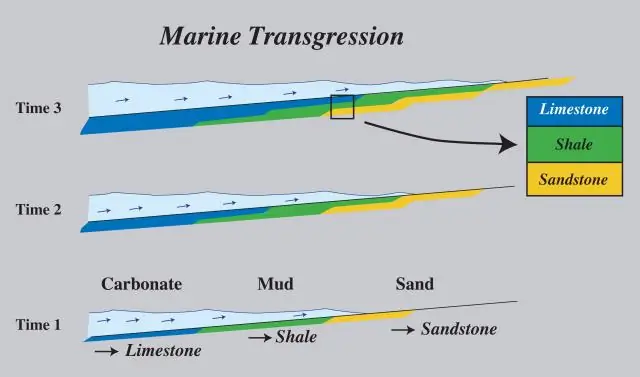
Трансгрессии и регрессии могут быть вызваны тектоническими событиями, такими как орогения, резкими изменениями климата, такими как ледниковые периоды, или изостатическими корректировками после удаления льда или наносов
Как рассчитать синусоидальную регрессию?
Синусоидальная регрессия. Отрегулируйте значения A, B, C и D в уравнении y = A * sin (B (x-C)) + D, чтобы синусоидальная кривая соответствовала заданному набору случайно сгенерированных данных. Если у вас есть хорошая функция, нажмите «Показать вычисленные», чтобы увидеть вычисленную линию регрессии. Используйте 'ctr-R' для создания новых точек данных и повторите попытку
Можем ли мы выполнить регрессию на нелинейных данных?
Нелинейная регрессия может соответствовать большему количеству типов кривых, но может потребоваться больше усилий как для поиска наилучшего соответствия, так и для интерпретации роли независимых переменных. Кроме того, R-квадрат недействителен для нелинейной регрессии, и невозможно вычислить p-значения для оценок параметров
Когда следует использовать корреляцию, а когда - простую линейную регрессию?
Регрессия в основном используется для построения моделей / уравнений для прогнозирования ключевого ответа Y на основе набора переменных-предикторов (X). Корреляция в основном используется для быстрого и лаконичного резюмирования направления и силы взаимосвязей между набором из 2 или более числовых переменных