
Оглавление:
- Автор Miles Stephen [email protected].
- Public 2023-12-15 23:40.
- Последнее изменение 2025-01-22 17:09.
Нелинейная регрессия может подходят для многих других типов кривых, но это жестяная банка требуется больше усилий как для поиска наиболее подходящего, так и для интерпретировать роль независимых переменных. Кроме того, R-квадрат недействителен для нелинейная регрессия , и невозможно вычислить p-значения для оценок параметров.
Таким образом, может ли регрессия быть нелинейной?
В статистике нелинейная регрессия это форма регресс анализ, в котором данные наблюдений моделируются функцией, которая является нелинейный сочетание параметров модели и зависит от одной или нескольких независимых переменных. Данные аппроксимированы методом последовательных приближений.
Можно также спросить, возводится ли квадрат r только для линейной регрессии? Общая математическая основа для р - в квадрате не работает правильно, если регрессионная модель не является линейный . Несмотря на эту проблему, большинство статистических программ по-прежнему рассчитывают р - в квадрате для нелинейных моделей. Если вы используете р - в квадрате выбрать лучшее модель , это приводит к правильному только модель 28-43% случаев.
В связи с этим, как вы рассчитываете нелинейную регрессию?
Если в вашей модели используется уравнение в виде Y = a0 + b1Икс1, это линейная регрессия модель. Если нет, то это нелинейный.
Y = f (X, β) + ε
- X = вектор из p предикторов,
- β = вектор k параметров,
- f (-) = известная функция регрессии,
- ε = член ошибки.
Какие бывают типы регрессии?
Типы регрессии
- Линейная регрессия. Это простейшая форма регрессии.
- Полиномиальная регрессия. Это метод подбора нелинейного уравнения путем взятия полиномиальных функций от независимой переменной.
- Логистическая регрессия.
- Квантильная регрессия.
- Хребтовая регрессия.
- Лассо-регрессия.
- Эластичная чистая регрессия.
- Регрессия основных компонентов (ПЦР)
Рекомендуемые:
Что такое таблица нелинейных функций?

Нелинейная функция - это функция, которая не является линейной, а график линейной функции представляет собой линию. Совершенно ясно, что график функции y = -x 2 + 4x не является линией, поэтому функция является нелинейной функцией
Как сделать синусоидальную регрессию на калькуляторе?
ВИДЕО Итак, как вы рассчитываете синусоидальную регрессию? Синусоидальная регрессия . Отрегулируйте значения A, B, C и D в уравнение y = A * sin (B (x-C)) + D, чтобы получить синусоидальный Кривая соответствует заданному набору случайно сгенерированных данных.
Как рассчитать нелинейную регрессию?

Если ваша модель использует уравнение в форме Y = a0 + b1X1, это модель линейной регрессии. Если нет, то это нелинейно. Y = f (X, β) + ε X = вектор из p предикторов, β = вектор из k параметров, f (-) = известная функция регрессии, ε = член ошибки
Какой метод классификации данных помещает равное количество записей или единиц анализа в каждый класс данных?

Квантиль. каждый класс содержит равное количество функций. Квантильная классификация хорошо подходит для линейно распределенных данных. Quantile назначает одинаковое количество значений данных каждому классу
Что вызывает морскую регрессию?
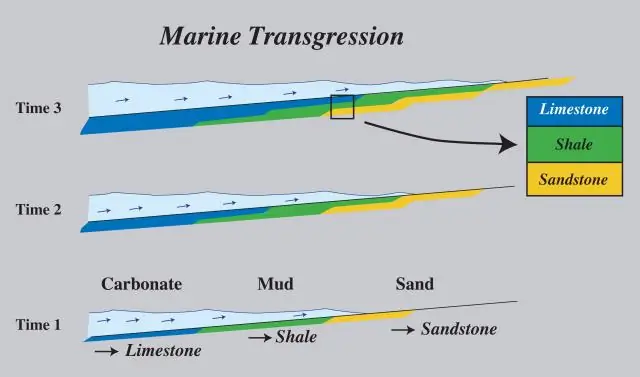
Трансгрессии и регрессии могут быть вызваны тектоническими событиями, такими как орогения, резкими изменениями климата, такими как ледниковые периоды, или изостатическими корректировками после удаления льда или наносов
