Оглавление:
Видео: Как решить систему из трех уравнений методом исключения?
2024 Автор: Miles Stephen | [email protected]. Последнее изменение: 2023-12-15 23:40
Выберите другой набор из двух уравнения , сказать уравнения (2) и (3), и Устранить та же переменная. Решать в система создан уравнения (4) и (5). Теперь подставим z = 3 в уравнение (4) найти y. Используйте ответы из шага 4 и замените их на любой уравнение с участием оставшейся переменной.
Соответственно, как решить систему уравнений методом исключения?
в устранение метод, который вы либо добавляете, либо вычитаете уравнения получить уравнение в одной переменной. Когда коэффициенты одной переменной противоположны, вы добавляете уравнения чтобы исключить переменную, и когда коэффициенты одной переменной равны, вы вычитаете уравнения чтобы исключить переменную.
Кроме того, что вы подразумеваете под устранением? Устранение это процесс избавления от чего-либо, будь то отходы, ошибки или конкуренция. Устранение происходит от латинского слова limen, которое средства порог. Римляне добавили букву «е» в начале и создали глагол «устранить», который средства прогнать или толкнуть порог и выйти за дверь.
Впоследствии возникает вопрос, как мне решить систему уравнений?
Вот как это происходит:
- Шаг 1: Решите одно из уравнений относительно одной из переменных. Решим первое уравнение относительно y:
- Шаг 2: подставьте это уравнение в другое уравнение и решите относительно x.
- Шаг 3: подставьте x = 4 x = 4 x = 4 в одно из исходных уравнений и решите относительно y.
Что значит решить систему уравнений?
А система уравнений представляет собой набор из двух или более уравнения с таким же набором неизвестных. В решение а система уравнений , мы пытаемся найти значения для каждого из неизвестных, которые удовлетворят все уравнение в система.
Рекомендуемые:
Как вы решаете систему линейных уравнений графически?
Чтобы решить систему линейных уравнений графически, мы графически отображаем оба уравнения в одной и той же системе координат. Решение системы будет в точке пересечения двух линий. Две прямые пересекаются в (-3, -4), что является решением этой системы уравнений
Как решить задачу линейного программирования методом углов?
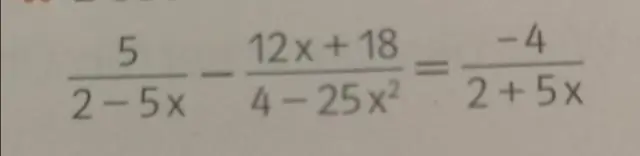
МЕТОД УГЛОВ Постройте график возможного множества (области) S. Найдите ТОЧНЫЕ координаты всех вершин (угловых точек) S. Вычислите целевую функцию P в каждой вершине Максимум (если он существует) - это наибольшее значение P в вершине. Минимум - это наименьшее значение P в вершине
Как можно алгебраически решить систему линейных уравнений?
Используйте исключение, чтобы найти общее решение в двух уравнениях: x + 3y = 4 и 2x + 5y = 5. x = –5, y = 3. Умножьте каждый член в первом уравнении на –2 (вы получите –2x - 6y = –8), а затем сложите члены в двух уравнениях. Теперь решите –y = –3 относительно y, и вы получите y = 3
Какими двумя способами можно решить систему уравнений алгебраически?
Когда даны два уравнения с двумя переменными, есть два алгебраических метода их решения. Один - замена, а другой - устранение
Как решить линейное уравнение методом исключения Гаусса?
Как использовать метод исключения Гаусса для решения систем уравнений Вы можете умножить любую строку на константу (кроме нуля). умножает строку три на –2, чтобы получить новую строку три. Вы можете переключить любые две строки. меняет местами первую и вторую строки. Вы можете сложить две строки вместе. складывает первую и вторую строки и записывает их во вторую строку