Оглавление:
Видео: Как решить задачу линейного программирования методом углов?
2024 Автор: Miles Stephen | [email protected]. Последнее изменение: 2023-12-15 23:40
THE МЕТОД УГЛОВ Изобразите допустимое множество (область), S. Найди ТОЧНЫЕ координаты всех вершин ( угол точек) S. Оцените целевую функцию P в каждой вершине. Максимум (если он существует) - это наибольшее значение P в вершине. Минимум - это наименьшее значение P в вершине.
Впоследствии также может возникнуть вопрос, какими методами можно решить LPP?
Графический метод решения задач линейного программирования
- Предлагаемые видео.
- Шаг 1. Сформулируйте задачу LP (линейное программирование).
- Шаг 2: Постройте график и нанесите линии ограничений.
- Шаг 3: Определите допустимую сторону каждой линии ограничения.
- Шаг 4: Определите область возможного решения.
- Шаг 5: Постройте целевую функцию на графике.
- Шаг 6: Найдите оптимальную точку.
что такое алгебраический метод в линейном программировании? Алгебра и симплекс Метод . А задача линейного программирования (LP) - это проблема оптимизации где все переменные непрерывны, цель - линейный (по отношению к переменным решения) функция, а допустимая область определяется конечным числом линейный неравенства или уравнения.
Здесь, как вы вычисляете угловые точки в линейном программировании?
В угловые точки - вершины допустимой области. Если у вас есть график системы линейный неравенства, то вы можете посмотреть на график и легко определить, где угловые точки находятся. Возможно, вам потребуется решить систему линейный уравнения для найти некоторые координаты точки в центре.
Что такое метод решения угловой точки?
В метод решения угловой точки состоит из четырех основных шагов:: Определение координат каждой вершины ( угловая точка ) возможного региона.: Вычислить значение целевой функции на каждом угловая точка .: Установите целевую функцию с максимальным значением.
Рекомендуемые:
Как решить уравнение линейного неравенства?
Есть три шага: переставьте уравнение так, чтобы «y» находилось слева, а все остальное - справа. Постройте линию 'y =' (сделайте ее сплошной линией для y≤ или y≥ и пунктирной линией для y). Заштрихуйте линию над линией для «больше чем» (y> или y≥) или ниже линии для 'меньше чем' (y <или y≤)
Каковы предположения линейного программирования?
Предположения линейного программирования, условия уверенности. Это означает, что числа в цели и ограничениях достоверно известны и меняются в течение изучаемого периода. Линейность или пропорциональность. Аддитивно. Делимость. Неотрицательная переменная. Конечность. Оптимальность
Как решить систему из трех уравнений методом исключения?
Выберите другой набор из двух уравнений, скажем, уравнения (2) и (3), и удалите ту же переменную. Решите систему, созданную уравнениями (4) и (5). Теперь подставим z = 3 в уравнение (4), чтобы найти y. Используйте ответы из шага 4 и подставьте в любое уравнение, включающее оставшуюся переменную
Что такое симплексный метод линейного программирования?
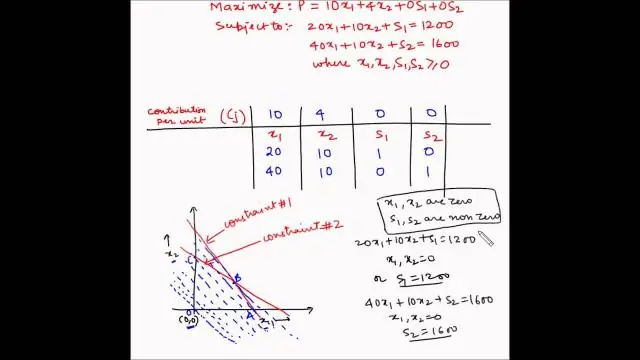
Симплексный метод. Симплексный метод, стандартный метод в линейном программировании для решения задачи оптимизации, обычно включающий функцию и несколько ограничений, выраженных в виде неравенств. Неравенства определяют многоугольную область (см. Многоугольник), и решение обычно находится в одной из вершин
Как решить задачу с 3-мя переменными?
Здесь в пошаговом формате показано, как решить систему с тремя уравнениями и тремя переменными: Выберите любые две пары уравнений из системы. Удалите одну и ту же переменную из каждой пары, используя метод сложения / вычитания. Решите систему двух новых уравнений, используя метод сложения / вычитания