Видео: Почему используются параметрические уравнения?
2024 Автор: Miles Stephen | [email protected]. Последнее изменение: 2023-12-15 23:40
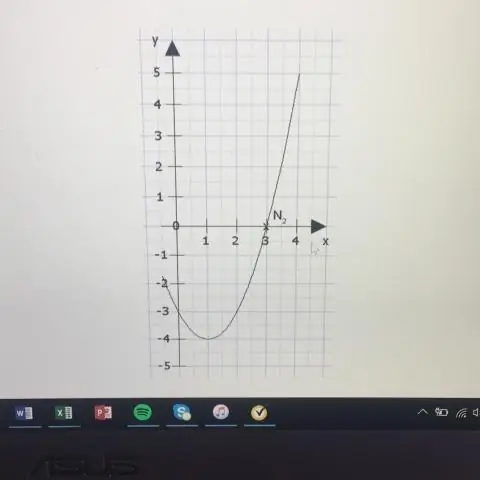
Одно из преимуществ параметрические уравнения это то, что они могут быть использовал для построения графиков кривых, которые не являются функциями, например единичной окружности. Еще одно преимущество параметрические уравнения в том, что параметр может быть использовал чтобы представить что-то полезное и, следовательно, предоставить нам дополнительную информацию о графике.
Также знаете, для чего используются параметрические уравнения?
Параметрические уравнения обычно привыкший выражают координаты точек, составляющих геометрический объект, например кривую или поверхность, и в этом случае уравнения все вместе называются параметрический представление или параметризация (или параметризация) объекта.
Кроме того, как работают параметрические уравнения? Параметрические уравнения используются, когда x и y напрямую не связаны друг с другом, а связаны через третий член. В этом примере положение автомобиля в направлении оси x изменяется линейно со временем, то есть график его функции представляет собой прямую линию.
Кроме того, что подразумевается под параметрической функцией?
Параметрические функции : Определение Параметрические функции находятся функции ряда координат (2 для 2-мерной плоскости, 3 для 3-D пространства и т. д.), где каждая из координат (x, y, z) выражается как другая функция некоторого параметра, например времени: x = f (t), y = g (t), z = h (t) и т. д.
Кто открыл параметрические уравнения?
Срок параметрический берет свое начало в математике, но ведутся споры о том, когда дизайнеры впервые начали использовать это слово. Дэвид Гербер (2007, 73), в его докторской диссертации Параметрический Практика, благодарит Мориса Рютера за то, что он впервые использовал этот термин в статье 1988 года, озаглавленной Параметрический Дизайн [1].
Рекомендуемые:
Почему ряды Фурье используются в технике связи?
Коммуникационная техника в основном имеет дело с сигналами, и, следовательно, сигналы бывают разных типов, таких как непрерывные, дискретные, периодические, непериодические и многие из многих типов. Теперь преобразование Фурье помогает нам преобразовать временную область сигнала в частотную область. Поскольку это позволяет нам извлекать частотные составляющие сигнала
Почему в некоторых элементах есть символы, в названии которых не используются буквы?
Другие несоответствия между именами и символами возникли в результате учёных, опирающихся на исследования классических текстов, написанных на арабском, греческом и латинском языках, а также из-за привычки «джентльменов-учёных» прошлых эпох использовать смесь двух последних языков в качестве «общего языка для всех». литераторы. " Символ Hg для ртути, например
Для чего используются полярные уравнения?
С точки зрения физика полярные координаты (rand θ) полезны при вычислении уравнений движения для множества механических систем. Довольно часто у вас есть объекты, движущиеся по кругу, и их динамику можно определить с помощью методов, называемых лагранжианом и гамильтонианом системы
Как буквальные уравнения используются в реальной жизни?
Решение буквальных уравнений часто полезно в реальных жизненных ситуациях, например, мы можем решить формулу для расстояния, d = rt, для r, чтобы получить уравнение для скорости. Нам потребуются все методы решения многошаговых уравнений. Решение для одной переменной в формуле
Почему важно учитывать множественность при определении корней полиномиального уравнения?
Например, количество раз, когда данное полиномиальное уравнение имеет корень в данной точке, является кратностью этого корня. Понятие множественности важно для правильного подсчета без указания исключений (например, двойные корни считаются дважды). Отсюда выражение «с учетом множественности»