Видео: Что такое уравнение Максвелла электромагнетизма?
2024 Автор: Miles Stephen | [email protected]. Последнее изменение: 2023-12-15 23:40
Уравнения Максвелла представляют собой набор из четырех дифференциальных уравнения которые составляют теоретическую основу для описания классических электромагнетизм : Закон Ампера: постоянные токи и изменяющиеся во времени электрические поля (последнее из-за Максвелла коррекция) создают магнитное поле.
Также знаете, как уравнения Максвелла описывают электромагнитные волны?
Уравнения Максвелла объясняют как эти волны может физически распространяться в космосе. Изменяющееся магнитное поле создает изменяющееся электрическое поле в соответствии с законом Фарадея. Этот вечный цикл позволяет этим волны , теперь известный как электромагнитное излучение , чтобы двигаться в пространстве со скоростью c.
Аналогично, что такое первое уравнение Максвелла? 1. Это уравнение утверждает, что эффективное электрическое поле через поверхность, охватывающую объем, равно полному заряду внутри объема. Чтобы запомнить целостную форму Уравнение Максвелла № 1, учтите, что заряд q, заключенный в объем, должен быть равен объемной плотности заряда r, умноженной на объем.
Во-вторых, в чем смысл уравнения Максвелла?
Уравнения Максвелла описывают, как электрические заряды и электрические токи создают электрические и магнитные поля. Кроме того, они описывают, как электрическое поле может создавать магнитное поле, и наоборот. Первое уравнение позволяет рассчитать электрическое поле, создаваемое зарядом.
Каковы четыре уравнения Максвелла?
Уравнения Максвелла представляют собой набор четыре дифференциал уравнения которые составляют теоретическую основу для описания классического электромагнетизма: закон Гаусса: электрические заряды создают электрическое поле. Закон Гаусса для магнетизма: нет магнитных монополей. Магнитный поток на замкнутой поверхности равен нулю.
Рекомендуемые:
Что такое уравнение квадратичной функции?
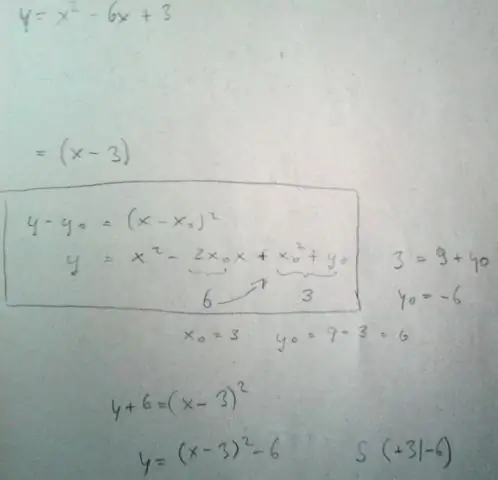
Квадратичная функция - это функция вида f (x) = ax2 + bx + c, где a, b и c - числа, у которых a не равно нулю. График квадратичной функции - это кривая, называемая параболой. Параболы могут открываться вверх или вниз и иметь различную «ширину» или «крутизну», но все они имеют одинаковую базовую U-образную форму
Что такое уравнение KW?
Kw = [H3O +] [OH-] = [H +] [OH-] = 1,001x10-14 (при 25 oC Kw зависит от температуры) (Использование [H3O +] эквивалентно использованию [H +].) Константа равновесия, Kw, называется константой диссоциации или константой ионизации воды
Что означают уравнения Максвелла?
Уравнения Максвелла описывают, как электрические заряды и электрические токи создают электрические и магнитные поля. Первое уравнение позволяет рассчитать электрическое поле, создаваемое зарядом. Второй позволяет рассчитать магнитное поле. Два других описывают, как поля «циркулируют» вокруг своих источников
Что такое уравнения Максвелла 4?
Уравнения Максвелла. Уравнения Максвелла представляют собой набор из четырех дифференциальных уравнений, которые составляют теоретическую основу для описания классического электромагнетизма: Закон Гаусса: электрические заряды создают электрическое поле. Электрический поток через замкнутую поверхность пропорционален заряду, заключенному в ней
Как появились уравнения Максвелла?
Свет - это электромагнитная волна: это было реализовано Максвеллом примерно в 1864 году, как только было обнаружено уравнение c = 1 / (e0m0) 1/2 = 2,998 · 108 м / с, поскольку к тому времени скорость света была точно измерена, и его согласие с c вряд ли было совпадением